Metode Eliminasi Gauss dan Gauss Jordan

Eliminasi Gauss Jordan beserta Contoh Penerapannya

1. Eliminasi Gauss-Jordan

Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan Operasi Baris Elementer.

Perhatikan ilutrasi berikut :


 

Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.

Ciri ciri Metode Gauss adalah 

 

  1. Jika suatu baris tidak semua nol, maka bilangan pertama yang tidak nol adalah 1 (1 utama)
  2. Baris nol terletak paling bawah
  3. 1 utama baris berikutnya berada dikanan 1 utama baris diatasnya
  4. Dibawah 1 utama harus nol
Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.
Metode ini digunakan untuk mencari invers dari sebuah matriks.
Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah
1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.
2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks
   A menjadi dalam bentuk baris eselon yang tereduksi

Contoh Soal Untuk Gauss dan Gauss jordan

Cari Nilai X1,X2,X3 pada persamaan dibawah ini menggunakan eliminasi gauss dan eliminasi gauss jordan

2X1 + X2 + 4X3 = 8
3X1 + 2X2 + X3 = 10
X1 + 3X2 + 3X3 = 8

Penyelesaian :

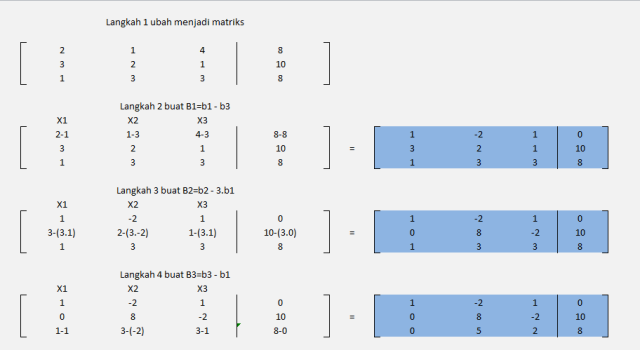
Eliminasi Gauss :

Langkah terakhir adalah substitusikan balik dari bawah jadi
X3 = 0.538
X2 – 0.25(X3) = 1.25
X2 = 1.25 + 0.25(0.538)
X2 = 1.384
X1 – 2X2 + X3 = 0
X1 = 2X2 – X3
X1 = 2(1.384) – 0.538
X1 = 2.23
Jadi X1 = 2.23, X2 = 1.384, X3 = 0.538

Dengan Eliminasi Gauss Jordan : 

Jadi Isinya sama seperti pada Eliminasi Gauss X1 = 2.23, X2 = 1.384, X3 = 0.538

 

Komentar

Posting Komentar

Postingan populer dari blog ini

pengunaan matriks pada bidang matriks

Gambar
 Pengunaan Matriks Pada Bidang Komputer dan Teknik Informatika I. Pendahuluan Tulisan ini berdasarkan studi literatur penerapan artikel - artikel yang berhubungan dengan penerapan mata kuliah Matriks . Mata kulia h Matriks merupakan mata kuliah dasar keahlian di program studi Teknik Informatika dan Sistem Informasi dan sangat berperan dalam menunjang pengetahuan bidang informatika dan sistem informasi. Dalam perkembangannya matriks banyak diterapkan dalam berbagai bidang untuk pemecahan masalah antara lain masalah teknik, ekonomi dan bisnis, kesehatan, komputer grafik, Global Positioning System (SPS),dan pemecahan persolan optimasi khususnya masalah penugasan.   II. Landasan Teori   a. Matriks     pengertian matriks Matrik s merupakan susunan sekelompok bilangan didalam suatu jajaran yang berbentuk persegi panjang dan diatur berdasarkan baris dan kolom yang kemudian diletakkan antara 2 tanda kurung. Tanda kurung yang dipakai untuk mengapit susunan an...
Baca selengkapnya

DETERMINAN MATRIKS DENGAN METODE CROUT DAN DOOLITTLE

Gambar
  METODE CROUT :              Langkah-langkah yang harus dilakukan pada Metode  Reduksi Crout adalah : -            Langkah pertama yang harus dilakukan adalah memasukkan ke-empat persamaan diatas ke dalam Matriks, dimana Matriksnya ber-orde 4x4.       -           Sehingga didapatlah nilai X 1  = 2, X 2  = -2, X 3  = 3, dan X 4  = -1.  Dengan menggunakan Metode Reduksi Crout kita langsung mendapatkan nilai X 1 , X 2 , X 3  dan X 4  nya dengan memasukkan rumus yang didapat dari persamaan Matriks A = [L].[U]. 2. METODE  DOOLITTLE : Suatu persamaan linear dapat diselesaikan secara langsung. Salah satu caranya adalah dengan menggunakan dekomposisi LU. Pada metode ini suatu sistem persamaan linier yang berbentuk:   difaktorisasi menjadi:   Pada deko...
Baca selengkapnya